A general treatment of snow microstructure exemplified by an improved relation for thermal conductivity

Abstract

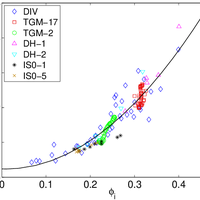
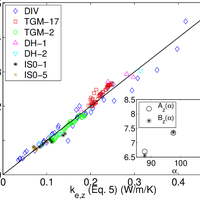
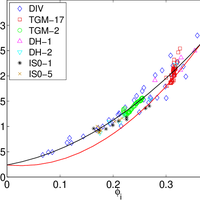
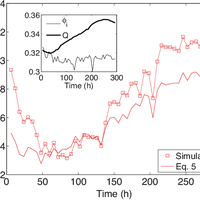
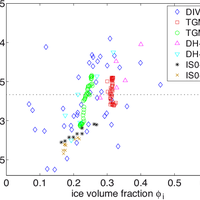
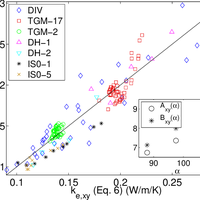
Finding relevant microstructural parameters beyond density is a longstanding problem which hinders the formulation of accurate parameterizations of physical properties of snow. Towards a remedy, we address the effective thermal conductivity tensor of snow via anisotropic, second-order bounds. The bound provides an explicit expression for the thermal conductivity and predicts the relevance of a microstructural anisotropy parameter Q, which is given by an integral over the two-point correlation function and unambiguously defined for arbitrary snow structures. For validation we compiled a comprehensive data set of 167 snow samples. The set comprises individual samples of various snow types and entire time series of metamorphism experiments under isothermal and temperature gradient conditions. All samples were digitally reconstructed by micro-computed tomography to perform microstructure-based simulations of heat transport. The incorporation of anisotropy via Q considerably reduces the root mean square error over the usual density-based parameterization. The systematic quantification of anisotropy via the two-point correlation function suggests a generalizable route to incorporate microstructure into snowpack models. We indicate the inter-relation of the conductivity to other properties and outline a potential impact of Q on dielectric constant, permeability and adsorption rate of diffusing species in the pore space. © 2013 Author(s).