Global glacier changes: A revised assessment of committed mass losses and sampling uncertainties

Abstract

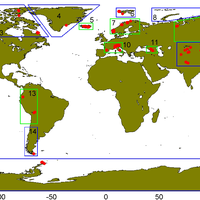
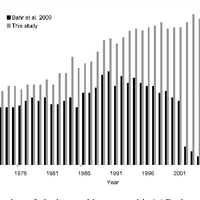
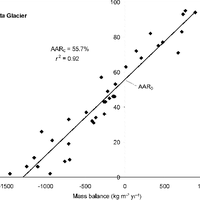
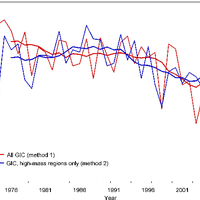
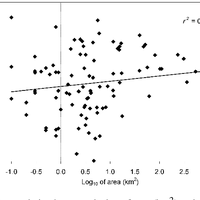
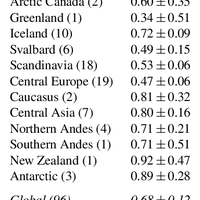
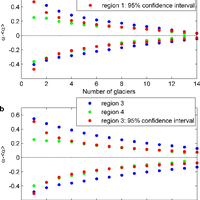
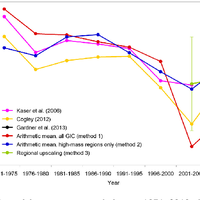
Most glaciers and ice caps (GIC) are out of balance with the current climate. To return to equilibrium, GIC must thin and retreat, losing additional mass and raising sea level. Because glacier observations are sparse and geographically biased, there is an undersampling problem common to all global assessments. Here, we further develop an assessment approach based on accumulation-area ratios (AAR) to estimate committed mass losses and analyze the undersampling problem. We compiled all available AAR observations for 144 GIC from 1971 to 2010, and found that most glaciers and ice caps are farther from balance than previously believed. Accounting for regional and global undersampling errors, our model suggests that GIC are committed to additional losses of 32 ± 12% of their area and 38 ± 16% of their volume if the future climate resembles the climate of the past decade. These losses imply global mean sea-level rise of 163 ± 69 mm, assuming total glacier volume of 430 mm sea-level equivalent. To reduce the large uncertainties in these projections, more long-term glacier measurements are needed in poorly sampled regions. © 2013 Author(s).