Abstract
Circular data are commonly encountered in the earth sciences and statistical descriptions and inferences about such data are necessary in structural geology. In this paper we compare two statistical distributions appropriate for complex circular data sets: the mixture of von Mises and the projected normal distribution. We show how the number of components in a mixture of von Mises distribution may be chosen, and how one may choose between the projected normal distribution and the mixture of von Mises for a particular data set. We illustrate these methods with a few structural geological data, showing how the fitted models can complement geological interpretation and permit statistical inference. One of our data sets suggests a special case of the projected normal distribution which we discuss briefly. © 2014 Author(s).
Figures
Register to see more suggestions
Mendeley helps you to discover research relevant for your work.
Cite
CITATION STYLE
Lark, R. M., Clifford, D., & Waters, C. N. (2014). Modelling complex geological circular data with the projected normal distribution and mixtures of von Mises distributions. Solid Earth, 5(2), 631–639. https://doi.org/10.5194/se-5-631-2014

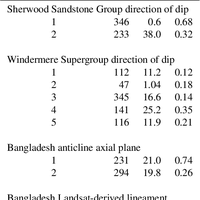
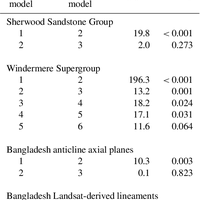
![Figure 1. Data: direction of dip for (a) the Sherwood Sandstone group (90 data) and (b) the Windermere Supergroup (572 data); orientations (doubled from the original range of [0,π ]) for (c) Bangladesh anticline axial planes (32 data) and (d) Bangladesh Landsat-derived lineaments (40 data). Note that segments of the rose diagrams are proportional to relative frequency within each data set separately, so are not comparable between data sets with respect to numbers of observations. If all data appeared within a single bin of the rose diagram then the corresponding segment would be equal in length to the radius of the circle.](https://s3-eu-west-1.amazonaws.com/com.mendeley.prod.article-extracted-content/images/505b0839-2942-3ef7-a819-9082323d3e0d/thumbnail-1cc4706a-8f8b-4061-b3ed-bf34d79c3a8f-0.png)
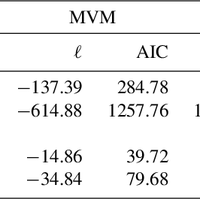
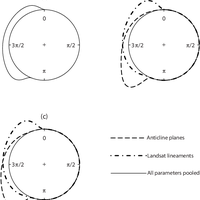
![Figure 2. Density of fitted projected normal distributions (PN) and a mixture of von Mises distributions (MVM) wrapped around the circle: direction of dip for (a) the Sherwood Sandstone group and (b) the Windermere Supergroup; orientations (doubled from the original range of [0,π ]) for (c) Bangladesh anticline axial planes and (d) Bangladesh Landsat-derived lineaments.](https://s3-eu-west-1.amazonaws.com/com.mendeley.prod.article-extracted-content/images/505b0839-2942-3ef7-a819-9082323d3e0d/thumbnail-087bedea-229c-40dd-9139-62e224a8549e-1.png)