A thermodynamic approach to link self-organization, preferential flow and rainfall-runoff behaviour

Abstract

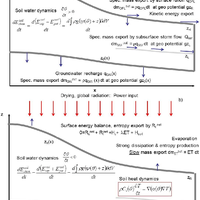
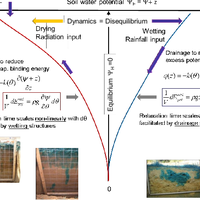
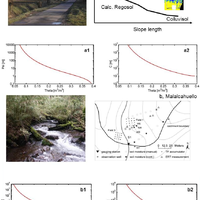
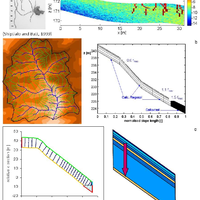
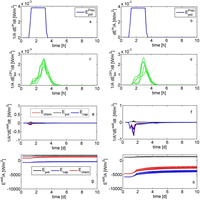
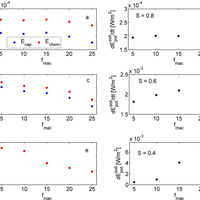
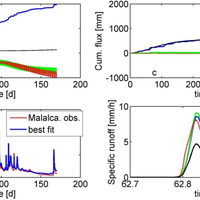
This study investigates whether a thermodynamically optimal hillslope structure can, if existent, serve as a first guess for uncalibrated predictions of rainfall-runoff. To this end we propose a thermodynamic framework to link rainfall-runoff processes and dynamics of potential energy, kinetic energy and capillary binding energy in catchments and hillslopes. The starting point is that hydraulic equilibrium in soil corresponds to local thermodynamic equilibrium (LTE), characterized by a local maximum entropy/minimum of free energy of soil water. Deviations from LTE occur either due to evaporative losses, which increase absolute values of negative capillary binding energy of soil water and reduce its potential energy, or due to infiltration of rainfall, which increases potential energy of soil water and reduces the strength of capillary binding energy. The amplitude and relaxation time of these deviations depend on climate, vegetation, soil hydraulic functions, topography and density of macropores. Based on this framework we analysed the free energy balance of hillslopes within numerical experiments that perturbed model structures with respect to the surface density of macropores. These model structures have been previously shown to allow successful long-term simulations of the water balances of the Weiherbach and the Malalcahuello catchments, which are located in distinctly different pedological and climatic settings. Our findings offer a new perspective on different functions of preferential flow paths depending on the pedological setting. Free energy dynamics of soil water in the cohesive soils of the Weiherbach is dominated by dynamics of capillary binding energy. Macropores act as dissipative wetting structures by enlarging water flows against steep gradients in soil water potential after long dry spells. This implies accelerated depletion of these gradients and faster relaxation back towards LTE. We found two local optima in macropore density that maximize reduction rates of free energy of soil water during rainfall-driven conditions. These two optima exist because reduction rates of free energy are, in this case, a second-order polynomial of the wetting rate, which implicitly depends on macroporosity. An uncalibrated long-term simulation of the water balance of the Weiherbach catchment based on the first optimum macroporosity performed almost as well as the best fit when macroporosity was calibrated to match rainfall-runoff. In the Malalcahuello catchment we did not find an apparent optimum density of macropores, because free energy dynamics of soil water during rainfall-driven conditions is dominated by increases of potential energy. Macropores act as dissipative drainage structures by enhancing export of potential energy. No optimum macropore density exists in this case because potential energy change rates scale linearly with the wetting rate. We found, however, a distinguished macroporosity that assures steady-state conditions of the potential energy balance of the soil, in the sense that average storage of potential energy is compensated by average potential energy export. This distinguished macroporosity was close to the value that yielded the best fit of rainfall-runoff behaviour during a calibration exercise and allowed a robust estimate of the annual runoff coefficient. Our findings are promising for predictions in ungauged catchments (PUB) as the optimal/distinguished model structures can serve as a first guess for uncalibrated predictions of rainfall-runoff. They also offer an alternative for classifying catchments according to their similarity of the free energy balance components. © Author(s) 2013.