Abstract
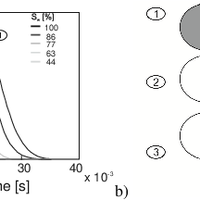
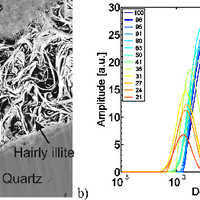
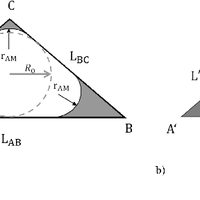
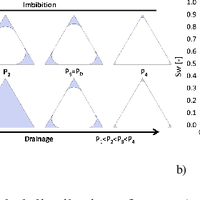
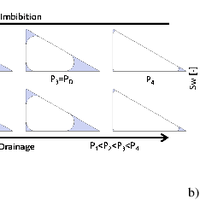
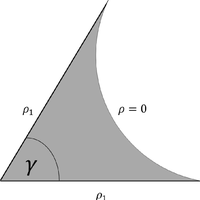
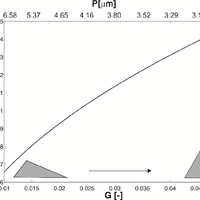
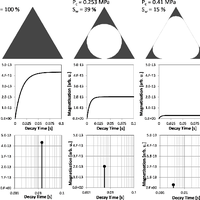
Nuclear magnetic resonance (NMR) relaxometry measurements are commonly used to characterize the storage and transport properties of water-saturated rocks. Estimations of these properties are based on the direct link of the initial NMR signal amplitude to porosity (water content) and of the NMR relaxation time to pore size. Herein, pore shapes are usually assumed to be spherical or cylindrical. However, the NMR response at partial water saturation for natural sediments and rocks may differ strongly from the responses calculated for spherical or cylindrical pores, because these pore shapes do not account for water menisci remaining in the corners of desaturated angular pores. Therefore, we consider a bundle of pores with triangular cross sections. We introduce analytical solutions of the NMR equations at partial saturation of these pores, which account for water menisci of desaturated pores. After developing equations that describe the water distribution inside the pores, we calculate the NMR response at partial saturation for imbibition and drainage based on the deduced water distributions. For this pore model, the NMR amplitudes and NMR relaxation times at partial water saturation strongly depend on pore shape, i.e., arising from the capillary pressure and pore shape-dependent water distribution in desaturated pores with triangular cross sections. Even so, the NMR relaxation time at full saturation only depends on the surface-to-volume ratio of the pore. Moreover, we show the qualitative agreement of the saturation-dependent relaxation-time distributions of our model with those observed for rocks and soils.
Figures
Register to see more suggestions
Mendeley helps you to discover research relevant for your work.
Cite
CITATION STYLE
Mohnke, O., Jorand, R., Nordlund, C., & Klitzsch, N. (2015). Understanding NMR relaxometry of partially water-saturated rocks. Hydrology and Earth System Sciences, 19(6), 2763–2773. https://doi.org/10.5194/hess-19-2763-2015