Abstract
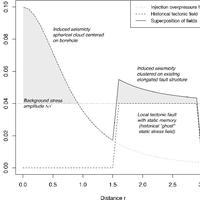
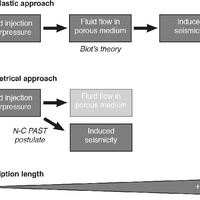
The standard paradigm to describe seismicity induced by fluid injection is to apply non-linear diffusion dynamics in a poroelastic medium. I show that the spatio-temporal behaviour and rate evolution of induced seismicity can, instead, be expressed by geometric operations on a static stress field produced by volume change at depth. I obtain laws similar in form to the ones derived from poroelasticity while requiring a lower description length. Although fluid flow is known to occur in the ground, it is not pertinent to the geometrical description of the spatio-temporal patterns of induced seismicity. The proposed model is equivalent to the static stress model for tectonic foreshocks generated by the Non-Critical Precursory Accelerating Seismicity Theory. This study hence verifies the explanatory power of this theory outside of its original scope and provides an alternative physical approach to poroelasticity for the modelling of induced seismicity. The applicability of the proposed geometrical approach is illustrated for the case of the 2006, Basel enhanced geothermal system stimulation experiment. Applicability to more problematic cases where the stress field may be spatially heterogeneous is also discussed..
Figures
Register to see more suggestions
Mendeley helps you to discover research relevant for your work.
Cite
CITATION STYLE
Mignan, A. (2016). Static behaviour of induced seismicity. Nonlinear Processes in Geophysics, 23(2), 107–113. https://doi.org/10.5194/npg-23-107-2016

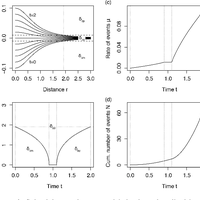
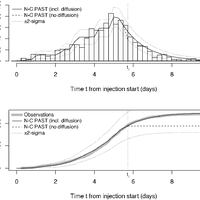
![Figure 2. 2006 Basel EGS stimulation experiment data with activation and quiescence envelope fits: (a) flow rate Q(t) (digitised from Häring et al., 2008); (b) spatio-temporal distribution of relocated induced seismicity (Kraft and Deichmann, 2014) with r the distance from the borehole. The activation and quiescence envelopes r∗ A (t) and r∗ Q (t) are defined from Eq. (13) with parameters 1̂σ∗ = 0.007 day−1 (dark curves) and 1t = 1/4 day. The light curves represent the range 1̂σ∗ ∈ [10−3,10−1] day−1 in 0.1 increments on the log10 scale. Points represent the induced earthquakes; which colour indicates how they are declared. (c) Score S = (wA+wQ)/2, with wA and wQ being the ratio of events of distance r ≤ r∗ A and r ≥ r∗ Q in the injection and bleeding-off phases, respectively. The vertical line represents 1̂σ∗ = 0.007 day−1.](https://s3-eu-west-1.amazonaws.com/com.mendeley.prod.article-extracted-content/images/362a45b5-ca65-364d-bc82-0662c9c5e7c7/thumbnail-383149a4-f31b-43f0-b379-52ee3b16a259-1.png)